F6. Cálculos y aplicaciones de las
fotografías aéreas
Como se ha dicho anteriormente existen dos tipos de fotografías: las
fotografías
aéreas convencionales (con proyección cónica) y las
ortofotografías
(con proyección plana). Con ambas se pueden realizar
operaciones, mediciones, análisis de localizaciones... es decir, todo
tipo de cálculos fotogramétricos, y además realizar mapas, estudios
biológicos, geológicos, edáficos, históricos, arqueológicos... Pero
puesto que los dos tipos de fotografías tienen distintas
proyecciones, los métodos a emplear son distintos.
A continuación se
muestran algunos cálculos y aplicaciones en ambos tipos de fotografías,
aunque actualmente ya no se suelen realizar medidas topográficas o
estudios generales directamente sobre fotografías aéreas convencionales
y utilizando estereoscopios, sino que normalmente se adquiere
directamente la ortofotografía o se transforma la fotografía con
proyección cónica en
una fotografía con proyección plana, y se realizan todos los cálculos a
partir de un visor
geográfico o un sistema de información geográfica
(SIG).
|
|
|
Cálculos
en fotografías aéreas:
Cálculo
de la altura del vuelo del avión:
La altura del vuelo del avión es un factor necesario para realizar
algunos cálculos fotogramétricos.
- En algunas fotografías
aéreas verticales suele estar indicado en el
margen de la imagen, pero si se desconoce se puede calcular teniendo en
cuenta la siguiente fórmula (en la que todos los valores deben estar en
la misma unidad de medida):
|
Altura del vuelo =
distancia focal x
fotoescala (el denominador de la escala de la foto)
|
Por ejemplo, si se quiere calcular la
altura del vuelo en una
fotografía que se ha realizado con una distancia focal de 150 mm y en
la que la fotoescala es 1:20.000, se aplica la fórmula: Altura
=
150 x 20.000, y el resultado es 3.000.000 mm. por lo tanto, el avión
volaba a una altura 3.000 metros mientras realizaba la foto.
- En
las ortofotografías
o en imágenes aéreas de
proyección plana: no se
puede calcular la altura del vuelo porque normalmente no se conoce la
distancia focal de la fotografía.
|
Cálculo
de la escala:
La escala es la relación de tamaño entre la imagen fotográfica y la
realidad. Por ello, es un factor muy importante, que si no aparece en
la imagen debe ser calculado.
- En fotografías aéreas
verticales: existen varios métodos para determinar la
escala sobre una fotografía aérea vertical, aunque hay que tener en
cuenta que dentro de una misma fotografía la escala varía de unas áreas
a otras (sobretodo si en la imagen hay un relieve muy acusado) debido a
las distorsiones que produce la proyección cónica. A continuación se
muestran los métodos más importantes:
a) Teniendo en cuenta la relación entre la distancia focal de las
lentes de la cámara y la altura del vuelo sobre el terreno, se puede
usar la siguiente fórmula (usando las mismas unidades de medida):
|
| Escala =
distancia focal de la
cámara / altura del vuelo sobre el plano del terreno |
es decir:
|
Escala= distancia
focal de la cámara /
(altura del vuelo - altitud media del terreno)
|
b) Se puede calcular midiendo la distancia
entre dos puntos en la realidad y entre esos dos mismos puntos sobre la
foto. Se pueden elegir elementos con medidas estándar (como las vías de
los ferrocarriles, las piscinas olímpicas, algunos campos de
deporte...). De esta forma se tendría que aplicar la siguiente fórmula
(usando las mismas unidades de medida):
|
Escala =
distancia entre 2 puntos
en la realidad / distancia entre esos 2 puntos en la foto
|
Si la distancia entre los dos puntos es de
500 m (50.000 cm) y la distancia entre esos dos puntos en la fotografía
es de 5 cm, la escala de la fotografía será 1:10.000 o 1/10.000.
Este método permite dar un valor aproximado de la escala, pero
solamente es válido para la zona de la foto en donde se encuentran los
dos puntos de referencia.
c) El siguiente método es similar al anterior pero en él los valores de
referencia se toman sobre un mapa o un plano con escala en donde se vea
la zona que aparece en la fotografía. Para ello se eligen dos
puntos identificables en el mapa y en la fotografía (la cúpula de una
iglesia, la intersección entre dos carreteras...), que estén situados a
la misma altitud, separados, y que la línea que los une pase por el
punto principal de la fotografía.
Después, se aplica la siguiente fórmula (usando las mismas unidades de
medida):
|
Escala de la foto =
(distancia entre dos
puntos medida en el mapa x escala del mapa) /
distancia entre esos mismos puntos medida sobre la foto
|
Si la distancia entre los dos puntos en el
mapa es de 140 mm, la escala del mapa es 1:25.000 y la distancia entre
los dos puntos en la fotografía mide 70 mm, la escala de la fotografía
o fotoescala será: 1:25.000 o 1/25.000.
Al igual que en el método b, el valor de la escala sólo es exacta en la
zona en donde están situados los puntos de referencia.
d) Existe otro método más exacto que consiste en calcular la escala
media de la fotografía, para ello se eligen tres puntos en
el mapa (A,
B y C) y en la fotografía aérea, de manera que formen un triángulo, más
o menos equilátero, que abarque casi toda la imagen. Después, se
calcula la escala aproximada de cada punto siguiendo el método “c” y se
hace la media teniendo en cuenta la siguiente fórmula:
|
Escala de la foto =
(escalaAB + escala AC +
escalaBC) / 3
|
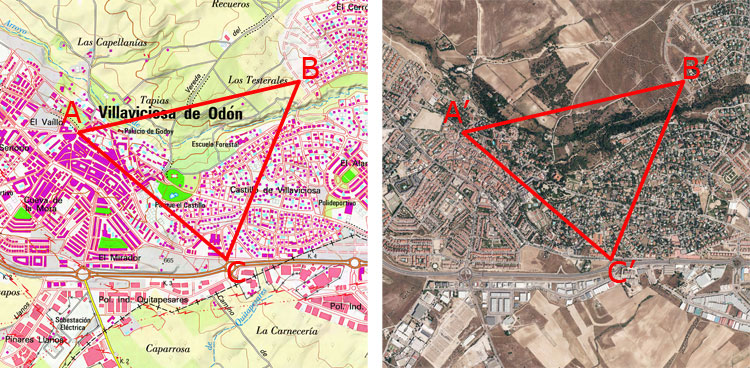 |
Ejemplo del cálculo
de la escala por el
método del triángulo
|
e) También existe otro método, similar al
anterior, pero en vez de que los puntos formen un triángulo, dibujan
una cruz. De esta forma, se realizan dos líneas, que pasen por el
centro de la fotografía y que se cortan formando un ángulo
recto, después se calculan las distancias de las líneas en el mapa y en
la fotografía aérea, y se obtiene la escala media:
|
Escala de la foto =
(escalaAB + escalaCD) /
2
|
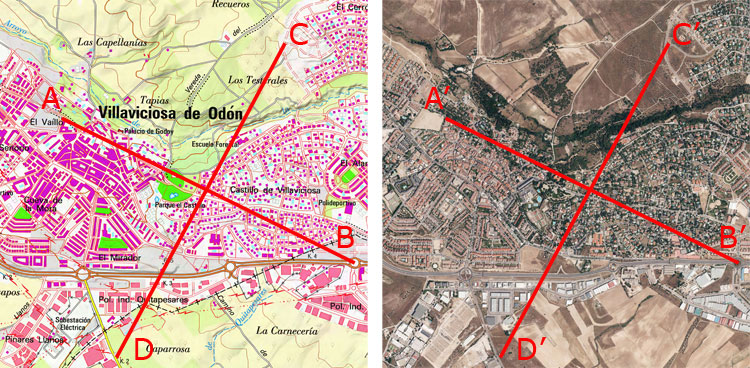 |
Ejemplo del cálculo
de la escala por el
método en cruz
|
- En ortofotografías
o en imágenes aéreas de
proyección plana: normalmente no es necesario calcular la
escala de la fotografía puesto que si se está empleando un programa SIG
o un visor geográfico, y si la imagen ya está georeferenciada, la
escala aparecerá automáticamente calculada por el programa. Si la
imagen no está georeferenciada, se puede georefenciar con un SIG
fácilmente teniendo en cuenta unos puntos claves de la imagen de los
que se conoce su posición exacta (como los vértices geodésicos).
En este tipo de imágenes, al tener una proyección plana, la escala es
uniforme. |
| |
| |
|
Continúa en la siguiente
página con el cálculo
de distancias, superficies y altura de los objetos...
|














